1. 자료의 수집과 정리
1.1. 모집단
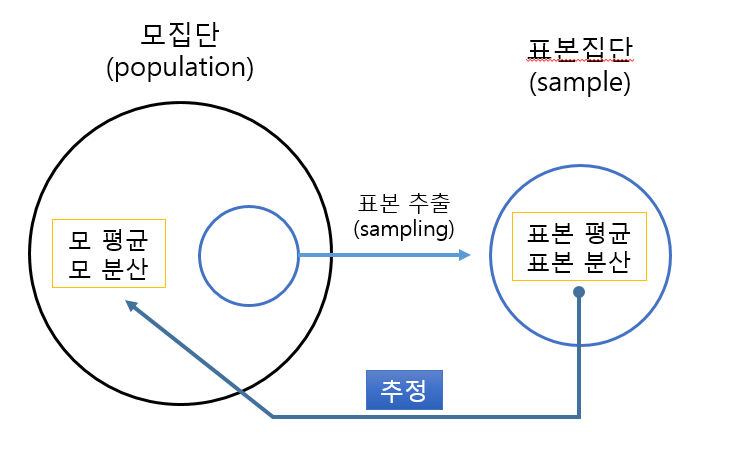
모집단(Population) 이란 조사대상 전체를 가리킨다.
우리나라 25세 이상 남자의 키 -> 우리나라 25세 이상 남자 모두를 조사해야 모집단 조건이 성립한다.
1.2. 표본
표본(Sample)은 모집단의 일부(부분집합)이다. 모집단이 너무 커서 전수조사가 불가능한경우 표본조사를 통해 모집단의 특성을 파악할 수 있다.
표본조사(Sampling)은 어느 한 쪽으로 치우치지 않도록 그 대상을 잘 선정하여야 한다.
표본추출의 목표는 모집단과의 편차를 최소화 하는 것이다.
표본을 선정에는 임의 표본(Random sampling) 방법이 많이 쓰인다.
표본을 적절히 추출하여 표본의 평균이나 분산을 구하여 이 결과 값으로 모평균과 모분산을 추정할 수 있다.
1.3 유효숫자 정리
유효숫자(Significant figures)는 수의 정확도에 영향을 주는 숫자이다.
평균을 구한 경우 원 데이터보다 소수점을 1개 정도 늘려준다.
10.5 12.3 15.1 -> 평균 = 12.6333 -> 소수점 정리 12.63
1.4. 변수
측정변수
-> 연속변수 - 중간 값이 무수히 많음. 예) 체중, 키 등
-> 불연속변수 - 정수로 표시되는 것. 예) 나이, 돼지의 한배새끼수, 산란수 등
순위변수 : 마라톤 골인순서 등
질적변수 : 성별, 모(털)색 등
1.5. 도수분포 [度數分布, frequency distribution]와 히스토그램
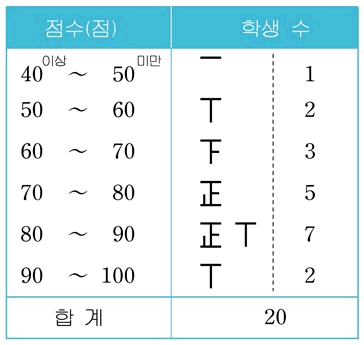
측정된 자료를 일정 구간으로 나누어 각 구간의 출현빈도를 기록한 표를 도수분포표라 한다.
네이버 http://terms.naver.com/entry.nhn?docId=926020&cid=47324&categoryId=47324
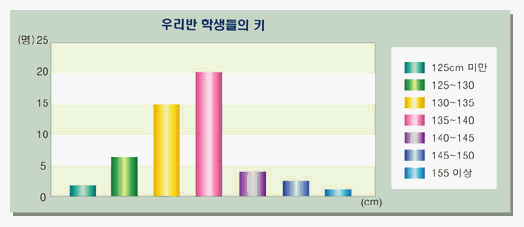
1.6 도수분포표 작성 실습
실습 결과물은 수업 종료시 이름 적어 제출
1. 수강생의 키와 몸무게의 히스토그램
주어진 엑셀 시트에 수강생 각자 자신의 나이, 성별, 키, 몸무게를 기록한다.
엑셀을 이용하여 돗수분포표를 작성한다.
2. 제시된 젖소의 체장에 대한 돗수분포표를 작성한다.
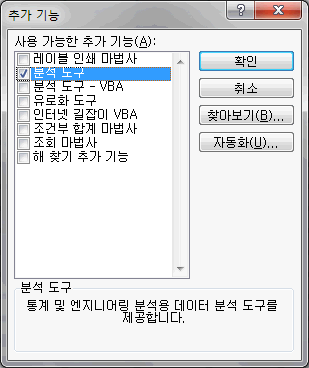
1.7 통계 분석을 위한 준비
오피스단추 -> 하단의 [ 엑셀옵션 ] 클릭
추가기능 클릭 -> 하단의 관리항목에서 엑셀 추가기능 선택 -> 이동 클릭
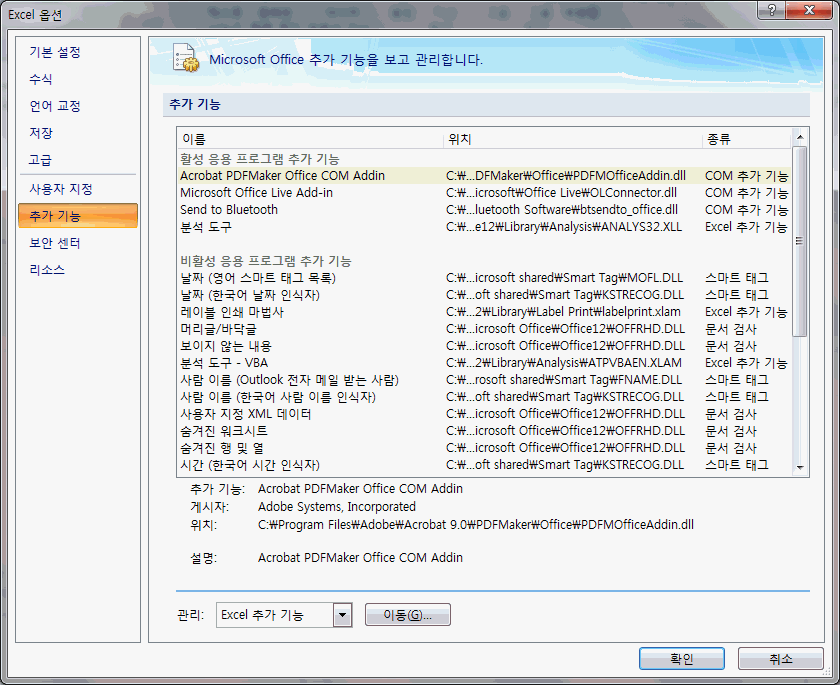
분석도구를 선택(클릭) -> [ 확인 ] 버튼 클릭
1.8 돗수분포표(히스토그램) 작성방법
엑셀 메뉴 데이터 -> 데이터분석 클릭 -> 히스토그램 선택 -> [ 확인 ] 클릭
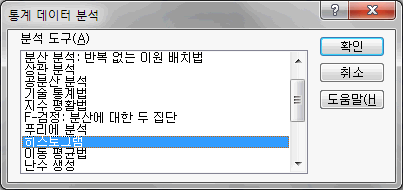
입력범위를 클릭하고 분석할 자료를 드래그하여 선택한다.
계급구간을 클릭하고 계급구간 자료를 드래그하여 선택한다.
출력옵션에서 출력범위를 선택하고 결과를 출력할 위치를 클릭하여 선택한다.
차트출력을 선택한다.
선택사항
출력 테이블에 빈도 내림차순으로 데이터를 표시하려면 파레토: 순차적 히스토그램 확인란을 선택합니다.
누적 백분율에 대한 출력 테이블 열을 생성하고 히스토그램 차트에 누적 백분율 선을 포함하려면 누적 백분율 확인란을 선택합니다.
출력 테이블에 포함된 히스토그램 차트를 생성하려면 차트 출력 확인란을 선택합니다.
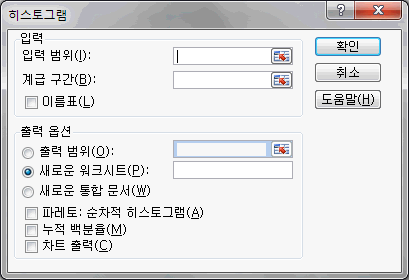
참고: 파레토의 법칙
하루종일 걸려오는 전화 중의 80%는 전화를 자주 하는 친근한 20%가 하는 것이다.
교수가 한 시간 강의 동안에 전달한 지식의 80%를 이해하는 학생은 불과 20%밖에 안 된다.
1897년 이탈리아 경제학자 빌프레도 파레토 (Vilfredo Pareto : 1848 ~ 1923)가 발견한 파레토 법칙.
파레토는 백화점의 하루 매상 중 80%는 그 백화점의 단골인 20%의 손님이 올린다는 것을 발견하면서, 이를 20대 80원칙이라고 명하였다.
인간사의 다양한 경제 통계 자료를 분석하면 20대 80원칙이 여러 분야에서 나타나고 있다.
20%의 인구가 80%의 돈을 가지고 있고,
20%의 근로자가 80%의 일을 하였으며,
20%의 소비자가 전체매출액의 80%를 차지하고 있었다는 것이다.
이는 어느 시대, 어느 국가를 막론하고 나타나는 현상이다.
개미를 관찰을 했는데, 개미 전체가 모두 열심히 일하는 것이 아니라 20% 정도의 개미만 열심히 일하고 있었죠. 그래서 열심히 일하는 개미만을 모아서 따로 일을 시켜보니, 그 안에서도 또다시 20% 정도만 열심히 일했습니다. 개미뿐만 아니라 벌에서도 이러한 현상을 확인하였다.
참고: 롱테일의 법칙
파레토 법칙이 부가 집중되는 20%에 중심을 두었다면, 반대로 80%의 작은 개인들이 20%의 소수보다 뛰어난 가치를 창출할 수 있다는 이론입니다.
온라인판매에서 두드러진 효과가 보임. - 아마존의 사업 모델(세상의 모든 책을 판매)
1.9 정규분포(Normal distribution)
정규분포
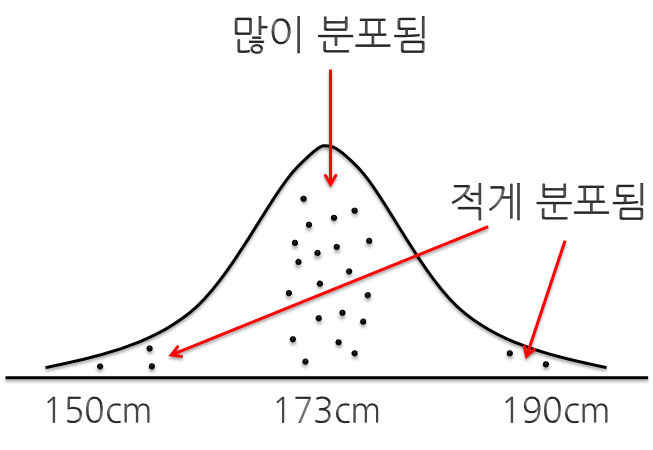
평균(m) 부근에 자료의 빈도가 많고, 평균에서 멀어질수록 자료의 빈도가 적어진다.
정규분포와 표준편차
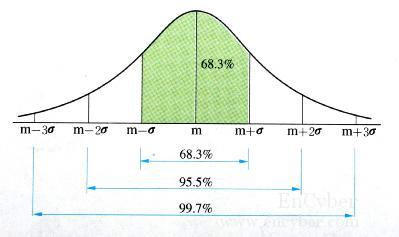
(평균 - 1 표준편차) ~ (평균 + 1 표준편차)의 면적은 전체의 68.3%
(평균 - 2 표준편차) ~ (평균 + 2 표준편차)의 면적은 전체의 95.5%
(평균 - 3 표준편차) ~ (평균 + 3 표준편차)의 면적은 전체의 99.7%
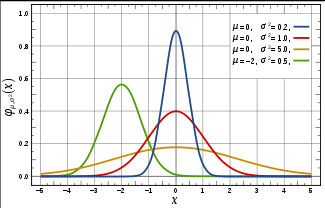
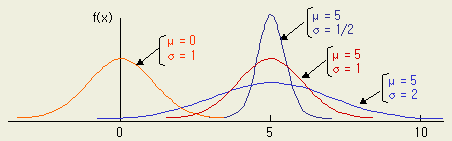
표준편차(분산)가 작으면 정규분포 곡선은 폭이 좁고 뽀족한 모양이 된다.
표준편차(분산)가 크면 정규분포 곡선은 폭이 넓고 평평한 모양이 된다.
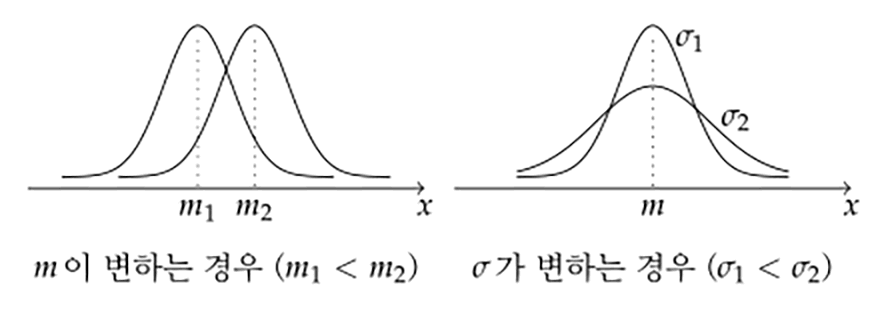
평균(m)이 변하면 정규분포 그래프의 위치가 좌우로 변경된다.
표준편차가 변하면 정규분포의 폭과 높이가 달라진다.